Smartphones offer many different sensors nowadays. Just have a look at the CAT S61 with its integrated thermal imaging camera, indoor air quality monitor... ok, I'll stop here. We just need one sensor to point at a screen: The gyroscope. Virtually every smartphone out there has it built in, MDN teaches us about detecting device orientation in Javascript. Can we somehow use this to make a smartphone behave like a laser pointer for a web app running on another, bigger and more stationary device?
Exploring the idea
I'll start by analyzing the problem: The screen of the bigger device can be thought of as a wall, the smartphone as a laser pointer. When I point a laser pointer at a wall, I see where I pointed it by having a little light dot appear on the wall. Technically, it doesn't matter how far away the wall is, I'll always see a point. The point appears because the ray of light is somehow "reflected" by the wall. For the use case at hand, it doesn't matter if the ray of light is reflected or simply goes through the wall, as long as I know where the metaphorical ray of light has hit the wall. To further illustrate the case I'll paint a little diagram:
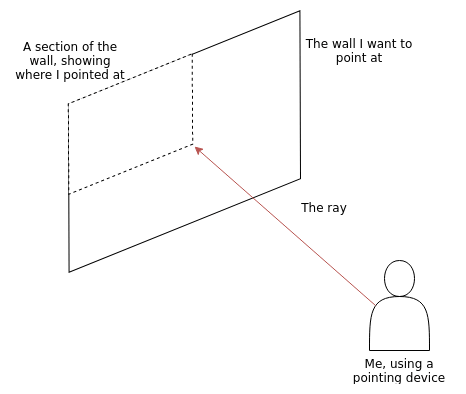
In order to reproduce the behaviour of a laser pointer in code, it would make sense to first map it mathematically. One mathematical construct that is suitable for this task are vectors, because vectors offer multiple tools for manipulating points and other constructs in a 3D space. The "ray of light" my smartphone emits can be thought of as a line in 3D space. The screen on the other hand can be considered a flat body or a so called plane.
Vectors, lines and planes - reality, but in numbers
If you're not familiar with vectors, lines and planes or if you think you need a refresher, I can recommend the intros created by Math is fun about vectors and further explanation by the Harvey Mudd College about lines and planes. To answer the question where on the wall my smartphone is pointed at, I need to answer these questions:
- Where is my smartphone?
- Where is the screen of my desktop?
- Which direction is my phone pointing at?
- Does the metaphorical ray of light hit the screen?
Technically, I only need to know where the smartphone is in relation to the screen. So for simplicity I fix its position one screen width away from the center of the screen, perpendicularlly. Let me again illustrate, but this time with vectors:
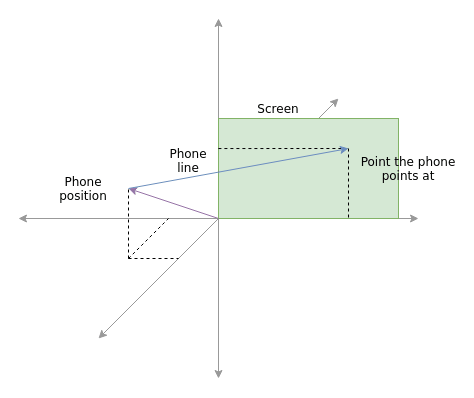
Nevermind that the position of the phone as well as that of the screen are not like described. They are only positioned as such for better visibility. I've already implemented the vectors, lines and planes as a little library available on npmjs. I'm going to use those to start implementing the parts needed to use my phone as a pointing device.
Setting things up - a line and a plane
Disclaimer: The following code examples are using ES6 and imply a webpack/babel setup. They're not exactly copy/paste-able, but they show how to work with the tools at hand.
The following code will likely run in the browser.
First, I'm going to instantiate a plane. I'm going to use the screen width and height as coordinates, so that every point on the screen I'm about to calculate actually contains the pixel coordinates. I'm going to use (0/0/0) as the first vector to keep my calculations as simple as possible. The two direction vectors are attached to this one in order to determine the position of the plane in 3D space. The direction vectors are going to be width and height of the screen.
import { Vector, Plane } from 'vanilla-vectors-3d'
const width = window.innerWidth
const height = window.innerHeight
const screenPlane = new Plane(
new Vector(0, 0, 0), // The first vector of the plain, usually where the two direction vectors are attached.
new Vector(width, 0, 0), // First direction vector
new Vector(0, height, 0) // Second direction vector
)Now I'm going to fix the position of the smartphone. I'd want the phone to be positioned at the center of the screen, one screen width away, as mentioned earlier. Also, the phone should point right at the screen. Then I instantiate a Line object. Also, I'm going to instantiate two axis which I can rotate the phone around. Those will also be lines.
import { Vector, Line } from 'vanilla-vectors-3d'
const phoneXPos = width / 2
const phoneYPos = height / 2
const phoneZPos = width
const phoneLine = new Line(
new Vector(phoneXPos, phoneYPos, phoneZPos),
new Vector(phoneXPos, phoneYPos, phoneZPos / 2) // divided by two, so the vector points in the right direction: at the screen
)
const xAxis = new Line(
new Vector(phoneXPos - 100, phoneYPos, phoneZPos), // Adjust x position so it goes right through the phone
new Vector(phoneXPos + 100, phoneYPos, phoneZPos)
)
const yAxis = new Line(
new Vector(phoneXPos, phoneYPos - 100, phoneZPos), // Adjust y position so it goes right through the phone
new Vector(phoneXPos, phoneYPos + 100, phoneZPos)
)And we're good to go. Next, I'm going to calculate an intersection point of the phoneLine and the screenPlane. This intersection point is exactly where the phone is pointing at on the screen. I only need the X and Y coordinates, as I'm going to display something on the screen. I'm projecting the 3D space to a 2D space.
const intersection = screenPlane.getIntersectionWith(phoneLine)
const screenX = intersection.x
const screenY = intersection.yThe following diagram should illustrate what I've programmed so far:
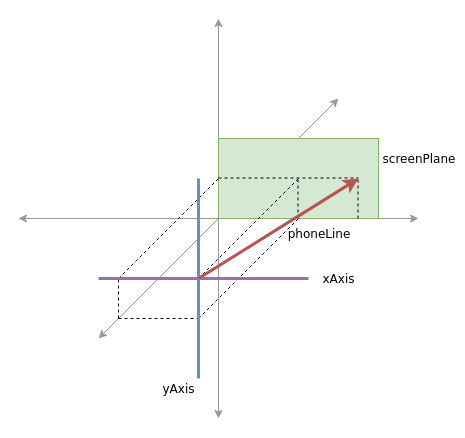
Marvelous! Next up: Movement.
Rotation
I assume that I'm getting the phone's gyroscope's angles from a function I call getGyroAngles(). I assume that this function returns the same object that a listener for JavaScript's deviceorientation event would receive. They're probably coming from some websocket or are being pushed to my desktop application via XHR and some server.
function getScreenCoords () {
const orientation = getGyroAngles() // The function I assume is returning the angles.
const phoneLinePrime = phoneLine
.rotateAroundLine(yAxis, orientation.alpha)
.rotateAroundLine(xAxis, 180 - orientation.beta)
const intersectionVector = screenPlane.getIntersectionWith(phoneLinePrime)
return {
x: Math.round(intersectionVector.x),
y: Math.round(intersectionVector.y)
}
}I can now use this function to update the position of an element regularly.
<style>
#myDot {
width: 10px;
height: 10px;
border-radius: 100%;
background-color: #f00;
position: absolute;
}
</style>
<span id="myDot" />
<script>
function updateDotPosition () {
const coords = getScreenCoords()
const dot = document.getElementById('myDot')
dot.style.left = coords.x
dot.style.bottom = coords.y
window.requestAnimationFrame(updateDotPosition)
}
updateDotPosition()
</script>And I'm done! Now, as soon as the orientation changes, the dot gets repositioned on the screen. The fact that I used vectors and geometry for that even makes it incredibly precise. So precise even, that for a tool that uses this we had to come up with a way to tolerate smaller movements, like the shaking of ones hand. The code is available as gyro-plane on npmjs as well.
Takaway thoughts
Using a phone as a pointing device is an interesting and challenging idea. It could be used for many different use cases. Using maths for this problem is something that came in very natural. It is another good example how maths actually describe the real world.
What use case do you see for such a technology?

